Rekursion und rekursive Formeln verstehen
Wiederholung
Iteration ist die Wiederholung eines Prozesses. Ein Schüler, der zur Schule geht, wiederholt den Prozess des Schulbesuchs jeden Tag bis zum Abschluss. Wir gehen mindestens ein- bis zweimal im Monat in den Supermarkt, um Produkte zu kaufen. Diesen Vorgang wiederholen wir jeden Monat. In der Mathematik folgt eine Fibonacci-Folge ebenfalls den Eigenschaften der Aufgabenwiederholung. Betrachten wir die Fibonacci-Folge, bei der die ersten beiden Zahlen 0 und 1 sind, alle anderen Zahlen sind die Summe der vorherigen beiden Zahlen.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
Iterationsschritte
Die Fibonacci-Formel kann geschrieben werden als:
F(n) = F(n – 1) + F(n – 2)
fibonacci(0) = 0
Fibonacci(1) = 1
Fibonacci (2) = Fibonacci (1) + Fibonacci (0) = 1 + 0 = 1
Fibonacci (3) = Fibonacci (2) + Fibonacci (1) = 1 + 1 = 2
Fibonacci (4) = Fibonacci (3) + Fibonacci (2) = 2 + 1 = 3
Fibonacci (5) = Fibonacci (4) + Fibonacci (3) = 3 + 2 = 5
Fibonacci (6) = Fibonacci (5) + Fibonacci (4) = 5 + 3 = 8
Der unten angegebene Algorithmus gibt die n-te Fibonacci-Zahl zurück.

Rekursion
Jedes Mal, wenn wir eine neue Fibonacci-Zahl (n-te Zahl) erhalten, ist diese n-te Zahl tatsächlich (n – 1)-te Zahl, wenn wir (n + 1)-te Fibonacci als unsere nächste n-te Fibonacci-Zahl finden. Wie wir die oben erwähnten Iterationsschritte sehen: wenn n = 2 dann
Fibonacci (2) = Fibonacci (2 – 1) + Fibonacci (2 – 2) = Fibonacci (1) + Fibonacci (0) = 1 + 0 = 1
Nun wollen wir fibonacci(3) generieren, also n = 3.
Fibonacci (3) = Fibonacci (3 – 1) + Fibonacci (3 – 2) = Fibonacci (2) + Fibonacci (1) = 1 + 1 = 2
Das heißt, jedes Mal, wenn n steigt, steigt auch der Wert des aktuellen (n – 1)ten und (n – 2)ten Fibonacci. Aber es ist ermüdend, die (n – 1)-te und (n – 2)-te Fibonacci für jedes n im Auge zu behalten. Wie wäre es, eine Methode zu schreiben, die sich selbst aufruft, um die Iterationsaufgabe selbst zu wiederholen?
Eine Methode, die sich selbst aufruft, wird als rekursive Methode bezeichnet. Eine rekursive Methode muss einen Basisfall haben, in dem das Programm aufhört, sich selbst aufzurufen. Unser Basisfall für Fibonacci-Reihen ist Fibonacci(0) = 0 und Fibonacci(1) = 1. Andernfalls nennt sich die Fibonacci-Methode zweimal – Fibonacci(n – 1) und Fibonacci (n – 2). Dann fügt es sie hinzu, um fibonacci(n) zu erhalten. Eine rekursive Methode zum Finden des n-ten Fibonacci kann geschrieben werden als –

Wenn wir genau hinschauen, folgt die Rekursion der Eigenschaft von stack. Es löst kleinere Teilprobleme, um die Lösung eines Problems zu erhalten. Für n > 1 führt es die letzte Zeile aus. Wenn also n = 6 ist, ruft die Funktion Fibonacci(6 – 1) und Fibonacci(6 – 2) auf und fügt sie hinzu. fibonacci(6 – 1) oder fibonacci(5) ruft und fügt fibonacci(5 – 1) und fibonacci(5 – 2) hinzu. Diese Rekursion wird fortgesetzt, bis 6 seinen Basisfallwert erreicht, der fibonacci(0) = 0 oder fibonacci(1) = 1 ist. 6). Unten ist eine Baumdarstellung der Rekursion.
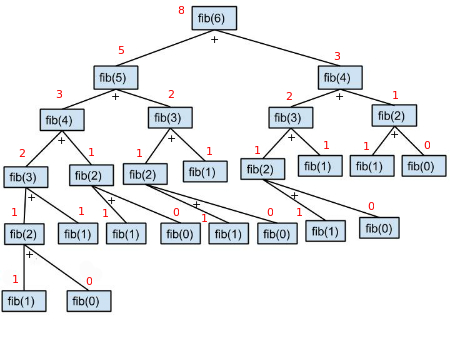
Wie wir sehen können, wie mächtig eine Rekursion sein kann. Nur eine einzige Codezeile erstellt den obigen Baum (letzte Zeile des obigen Codes einschließlich der Basisfälle). Die Rekursion behält einen Stapel bei und geht tiefer, bis sie den Basisfall erreicht. Dynamische Programmierung (DP): Rekursion ist leicht zu verstehen und zu programmieren, kann jedoch in Bezug auf Zeit und Speicher teuer sein. Sehen Sie sich den Rekursionsbaum unten an. Der linke Teilbaum beginnend mit fib(4) und der rechte Teilbaum beginnend mit fib(4) sind genau gleich. Sie erzeugen das gleiche Ergebnis, nämlich 3, führen aber dieselbe Aufgabe zweimal aus. Wenn n eine große Zahl ist (Beispiel: 500000), kann die Rekursion ein Programm sehr langsam machen, da es dieselbe Unteraufgabe mehrmals aufrufen würde.
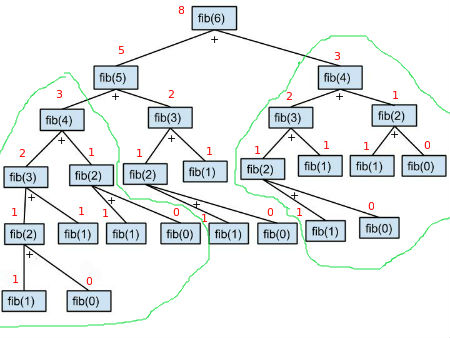
Um dieses Problem zu vermeiden, kann dynamische Programmierung verwendet werden. In der dynamischen Programmierung können wir zuvor gelöste Teilaufgaben verwenden, um zukünftige Aufgaben desselben Typs zu lösen. Dies ist eine Möglichkeit, die Aufgabe zur Lösung des ursprünglichen Problems zu reduzieren. Lassen Sie uns ein Array-Fib haben[] wo wir zuvor gelöste Teilaufgabenlösungen speichern. Wir wissen bereits, dass fib[0] = 0 und fib[1] = 1. Speichern wir diese beiden Werte. Was ist nun der Wert von fib[2]? Als fib[0] = 0 und fib[1] = 1 wurde bereits gespeichert müssen wir nur sagen fib[2] = fib[1] + fib[0] Und das ist alles. Wir können fib generieren[3], fib[4], fib[5], ……, fib[n] auf die gleiche Weise. Zuvor gelöste Teilaufgaben werden aufgerufen, um die nächste Teilaufgabe zu erhalten, bis die ursprüngliche Aufgabe nicht gelöst wurde, wodurch redundante Berechnungen reduziert werden.